Laplace's law of succession

Suppose that every time there is an opportunity for an event to happen, then it occurs with unknown probability [math]p[/math]. Laplace's law of succession states that, if before we observed any events we thought all values of [math]p [/math] were equally likely, then after observing [math]r[/math] events out of [math]n[/math] opportunities a good estimate of [math]p[/math] is [math]\hat{p} = (r+1)/(n+2)[/math].

When the event keeps on occurring

Suppose we have observed [math]n [/math] events in [math]n [/math] opportunities. Then the probability of this sequence is [math]p^n[/math]. We need to turn this into a distribution for [math]p[/math] that represents reasonable belief: this requires Bayes theorem but, if we believe all value of [math]p [/math] were equally plausible before making any observations, the distribution for [math]p [/math] is just proportional to [math]p^n[/math]. Probability distributions must integrate up to 1, and [math]\int_0^1 p^n dp= 1/(n+1)[/math], and so the full probability distribution for [math]p [/math] must be of the form
[math]f(p) = (n+1)\,p^n[/math], drawn below for different values of [math] n[/math].

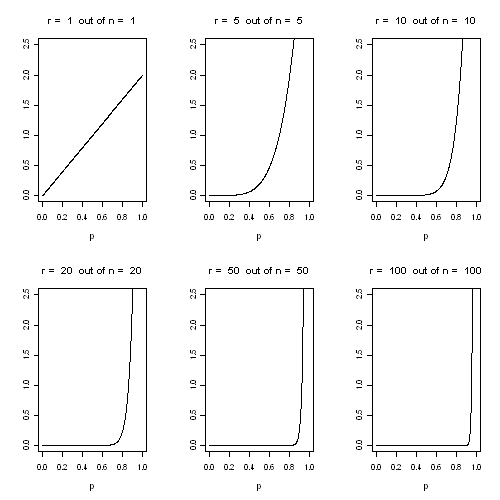
Probability distribution for various values of the chance [math]p [/math] of an event occurring, following [math]n [/math] events in [math]n [/math] opportunities

We can see that as the event occurs again and again, we become more confident that the underlying chance is near 1. To find the expectation of this distribution, we need to work out
[display]\int_0^1 \,\,p \,\,f(p) dp = (n+1) \,\,\int_0^1 \,\,p^{n+1} \,\,dp= \frac{(n+1)}{(n+2)}[/display].

When the event does not occur every time

Suppose we have observed [math]r [/math] events in [math]n [/math] opportunities. Then the probability of this particular sequence is [math]p^r \,\,(1-p)^{n-r}[/math]. Again, if we believe all value of [math]p [/math] were equally plausible before making any observations, the distribution for [math]p [/math] is just proportional to [math]p^r \,(1-p)^{n-r}[/math]. Probability distributions must integrate up to 1, and a standard result is that
[display]\int_0^1 \,\, p^r \,(1-p)^{n-r} dp = \frac{r!(n-r)!}{(n+1)!}. [/display]
So the full probability distribution for [math]p [/math] must be of the form
[display]f(p) = \frac{(n+1)!}{r!(n-r)!} \,\,p^r \,\,(1-p)^{n-r},[/display]
drawn below for different values of [math] r[/math] and [math] n[/math].

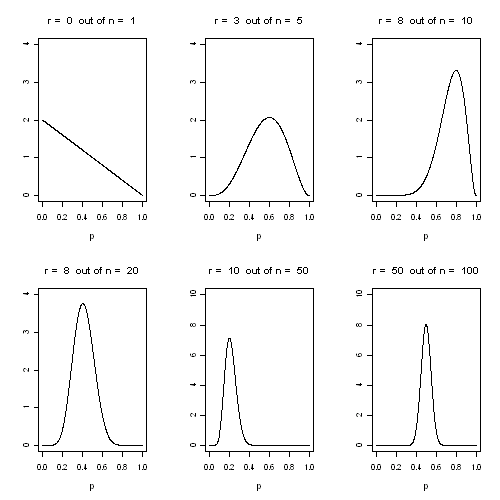
Probability distribution for various values of the chance [math]p [/math] of an event occurring, following [math]r [/math] events in [math]n [/math] opportunities (note change in vertical scale)

To find the expectation of this distribution, we need to work out
[display]\int_0^1 \,p \,f(p) dp = \frac{(n+1)!}{r!(n-r)!} \int_0^1\,\,p^{r+1} \,(1-p)^{n-r} dp= \frac{(n+1)!}{r!(n-r)!} \,\, \frac{(r+1)!(n-r)!}{(n+2)!}= \frac{(r+1)}{(n+2)}[/display].