Pure Randomness in Art
As of the 23rd May 2022 this website is archived and will receive no further updates.
understandinguncertainty.org was produced by the Winton programme for the public understanding of risk based in the Statistical Laboratory in the University of Cambridge. The aim was to help improve the way that uncertainty and risk are discussed in society, and show how probability and statistics can be both useful and entertaining.
Many of the animations were produced using Flash and will no longer work.
 This article is based on a talk I gave at the recent John Cage exhibition in Kettles Yard gallery in Cambridge. Cage is perhaps best known for his avant-garde music, particularly his silent 1952 composition 4′33″ but also for his use of randomness in “aleatory music”.
This article is based on a talk I gave at the recent John Cage exhibition in Kettles Yard gallery in Cambridge. Cage is perhaps best known for his avant-garde music, particularly his silent 1952 composition 4′33″ but also for his use of randomness in “aleatory music”.
He also used randomness in his art. The Kettles Yard exhibition featured wonderful film of assistants reading computer-generated random numbers off a list which determined which of a row of stones were to be chosen, which brush to use, and the position of the stone on the paper; Cage finally paints around the stone, stands back and announces the results as ‘beautiful’. He also dictated the use of chance in the form of the exhibition, and Kettles Yard used computer-generated coordinates to determine the heights and positions of the pictures, removing and adding pieces during the exhibition using a random process.

Cage at Kettles Yard
See more arrangements of this work at the Kettles Yard facebook gallery.
In this process Cage is deliberately sacrificing some control - “I use chance operations instead of operating according to my likes and dislikes”. It is important to distinguish this approach from artists such as Jackson Pollock, whose work may at first appear haphazard but is a form of controlled expression. Pollock claimed that no chance was involved: “When I am painting I have a general notion of what I am about. I can control the flow of paint, there is no accident just as there is no beginning and no end” and in these paintings “I want to express my feelings rather than illustrate them.”
Other artists using artificial randomising devices as an integral part of their work include Ellsworth Kelly in Spectrum Colors Arranged by Chance II, 1951, while Kenneth Martin’s Chance and Order pictures were created in the following way: “The points of intersection on a grid of squares are numbered and the numbers are written on small cards and picked at random…A line is made between each successive pair of numbers as they are picked out”.

Kenneth Martin's Chance and Order
I am personally not so keen on Cage’s work, but was awed by an exhibition at the Serpentine Gallery in London of Gerhard Richter’s “4900 Colours: Version II”. This is based on 196 panels each comprising a 5 x 5 square. A computer program assigned a colour to each square drawn at random from a palette of 25 colours. The 196 panels can be put together to form one huge display, or in the Serpentine exhibition were arranged at random in sets of four to form 49 10x 10 displays. The video below shows the hanging process.
It is remarkable how ‘non-random’ the panels look, with some dominated by particular colours which are often placed next to each other. But the whole point of ‘pure’ randomness is that apparent patterns are expected to occur. The number of times that lottery balls turn up makes a predictable pattern, while when flipping a coin 20 times there is a 77% chance of a run of at least 4 heads or tails.
My examples of Richter-like displays are shown below using 9 colours chosen at random within each square of a 9 x 9 grid. There are often apparent clusters and patterns in the colours. Can you spot the fake piece of random art?

Four 9 by 9 colour squares - can you spot which one is not random?
Other uses of pure randomness
Randomness has been extensively used in designing experiments in agriculture and medicine. When comparing treatments, whether fertilizers or medicinal drugs, we want to make sure that the differences observed are due to the intervention and not due to the land or the patients being different. In medicine we generally simply randomly allocate patients to treatments: in agriculture a more structured approach is possible.
A classic design is the Latin square. Suppose one wanted to compare 8 different fertiliser regimes, then a field can be divided up into 64 squares arranged as an 8x8 grid, and one of 8 regimes applied once in each row and column in order to make sure that the different ‘treatments’ are balanced across the field. Examples of 8x8 and 9x9 latin squares from Fisher and Yates' book of statistical tables (1938) are shown below, in which the letters correspond to a treatment.
| A | B | C | D | E | F | G | H |
| B | C | A | E | F | D | H | G |
| C | A | D | G | H | E | F | B |
| D | F | G | C | A | H | B | E |
| E | H | B | F | G | C | A | D |
| F | D | H | A | B | G | E | C |
| G | E | F | H | C | B | D | A |
| H | G | E | B | D | A | C | F |
$8\times 8$
| A | B | C | D | E | F | G | H | I |
| B | C | E | G | D | I | F | A | H |
| C | D | F | A | H | G | I | E | B |
| D | H | A | B | F | E | C | I | G |
| E | G | B | I | C | H | D | F | A |
| F | I | H | E | B | D | A | G | C |
| G | F | I | C | A | B | H | D | E |
| H | E | G | F | I | A | B | C | D |
| I | A | D | H | G | C | E | B | F |
$9\times 9$
Examples of Latin Squares
Gonville and Caius College in Cambridge has a stained glass Latin Square in tribute to Fisher – I have copied this idea and constructed the 8 x 8 example above as a stained glass panel.

The author's rendition of Fisher and Yates in stained glass
This is a very different process from Richter’s. The design is highly structured, with the only randomisation being the choice of a particular latin square and the allocation of colours/crops to the letters A, B, C,...
A special Latin Square
The 2nd example (top right) of my ‘random art’ is the odd one out, and is highly non-random. It is a Latin square but the image below reveals it to have been carefully chosen to have rather special properties.

A special latin square
We quickly see that it is a solution to a Sudoku puzzle, with each colour appearing once and only once in each 3x3 subsquare. Sudoku can be said to have arisen in agricultural field experiments. Behrens introduced the idea of gerechte designs in 1956, in which each of n crop varieties would also appear only once in a sub-area of size n, and in 1977 John Nelder posed the problem of uniquely completing a Latin square from a critical set of entries. Howard Garns put these ideas together in 1979 as a number place puzzle, which in 1986 became popular in Japan under the name Sudoku. A Sudoku puzzle is therefore, in formal terms, a critical set for a gerechte design for the 9x9 grid partitioned into 3x3 subsquares.
But the example shown above is particularly special. We first need to define a ‘broken row’ and ‘broken column’. A broken row, for example, is a set of 3 corresponding mini-rows in 3 vertical sub-squares as shown in the figure below.
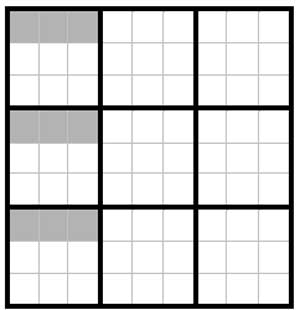
Broken rows
The image shown above represents a symmetric Sudoku solution: each colour occurs once in each column, row, 3x3 sub-square, position in a sub-square, broken row and broken column. Bailey, Cameron and Connelly recently proved there are only two such patterns using an elegant combination of coordinate geometry and coding theory: it is left as an exercise for the reader to show that the pattern shown above can be completed after specifying the 14 entries shown below.
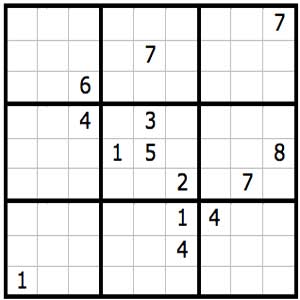
The critical set for one of the two symmetric Sudoku solutions
All I now have to do is make this into a stained glass window.
Acknowledgements
I would like to thank Elizabeth McKellar for all her help in preparing the talk.
- Log in to post comments

Comments
Glenn Westmore
Wed, 27/01/2016 - 1:24pm
Permalink
Graeco-Latin Squares