What does a 13% increased risk of death mean?

A recent study from Harvard reported that people who ate more red meat died at a greater rate. This provoked some wonderful media coverage: the Daily Express said that ‘if people cut down the amount of red meat they ate – say from steaks and beefburgers –to less than half a serving a day, 10 per cent of all deaths could be avoided, they say”.

Well it would be nice to find something that would avoid 10% of all deaths, but sadly this is not what the study says. Their main conclusion is that an extra portion of red meat a day, where a portion is 85g or 3 oz - a lump of meat around the size of a pack of cards or slightly smaller than a standard quarter-pound burger – is associated with a ‘hazard ratio’ of 1.13, that is a 13% increased risk of death. But what does this mean? Surely our risk of death is already 100%, and a risk of 113% does seem very sensible? To really interpret this number we need to use some maths.

Let’s consider two friends –Mike and Sam, both aged 40, with the same average weight, alcohol consumption, amount of exercise, family history of disease, but not necessarily exactly the same income, education and standard of living. Meaty Mike eats a quarter-pound burger for lunch Monday to Friday, while Standard Sam does not eat meat for weekday lunches, but otherwise has a similar diet to Mike (we are not concerned here with their friend Veggie Vern, who doesn’t eat meat at all.)

Each one faces an annual risk of death, whose technical name is their ‘hazard’. Therefore a hazard ratio of 1.13 means that, for two people like Mike and Sam who are similar apart from the extra meat, the one with the risk factor – Mike - has a 13% increased annual risk of death over the follow-up period (around 20 years).

However, this does not mean that he is going to live 13% less, although this is how some people interpreted this figure. So how does it affect how long they each might live? For this we have to go to the life-tables provided by the Office of National Statistics.

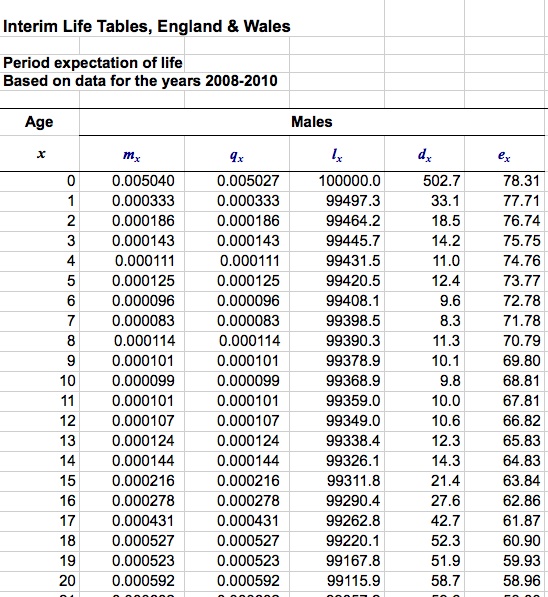
Fig 1 shows a piece of the male life-table for 2008-2010 for England and Wales. The $l_x$ column shows how many of 100,000 new boy babies we would expect to live to each birthday $x$, while the $q_x$ column shows the proportion of males reaching age $x$ that we expect to die before their $(x+1)$th birthday – this is the hazard. It follows that $d_x$ is the number of males that are expected to die in their $x$th year, where $d_x = q_x l_x$: for example, out of 100,000 male live-births, around 503 are expected to die in their first year, but only 33 between their 1st and 2nd birthdays. The column headed $e_x$ shows the life-expectancy of someone reaching their $x$th birthday – this is approximately $\sum_{t=x}^M t d_t/ \sum_{t=x}^M d_t + 0.5$, carrying out the summations from age $x$ up to the oldest age $M$ you expect anyone to live, say 110.

Consulting the original life-table shows that an average 40-year old man can expect to live another 40 years. This is not, of course, how long he will live – it may be less, it may be more, 40 years is the average. It also is based on the current hazards $q_x$ – in fact we can expect things to improve as he gets older. Life tables that take into account expected improvements in hazards are known as ‘cohort’ life-tables, rather than the standard ‘period’ life-table, and according to the current cohort life-table for England and Wales, a 40-year-old can expect to live another 46 years.

Since we assume Sam is consuming an average amount of red meat, we shall take him as an average man. We can see the effect of a hazard-ratio of 1.13 by multiplying all the $q_x$ column by 1.13 and recalculating $d_x$ and then life-expectancy from aged 40, which gives us 39 extra years for Mike. So the extra meat is associated, but did not necessarily cause, the loss of one year in life-expectancy.

Over 40 years this is 1/40th difference, or roughly one week a year or ½ hour per day. So a life-long habit of eating burgers for lunch is associated with a loss of ½ hour a day, considerably more than it takes to eat the burger. As we showed in our discussion of Microlives a half-hour off your life-expectancy is also associated with 2 cigarettes and each day of being 5 Kg overweight.

Of course we cannot say that precisely this time will be lost, and we cannot even be very confident that Mike will die first. An extremely elegant mathematical result, proved here , says that if we assume a hazard ratio $h$ is kept up throughout their lives, the odds that Mike dies before Sam is precisely $h$. Now odds is defined as $p/(1-p)$, where $p$ is the chance that Mike dies before Sam. Hence
$$ p = h/(1+h) = 0.53.$$
So there is only a 53% chance that Mike dies first, rather than 50:50. Not a big effect.

Finally, neither can we say the meat is directly causing the loss in life expectancy, in the sense that if Mike changed his lunch habits and stopped stuffing his face with a burger, his life-expectancy would definitely increase. Maybe there’s some other factor that both encourages Mike to eat more meat, and leads to a shorter life.

It is quite plausible that income could be such a factor – lower income in the US is both associated with eating more red meat and reduced life-expectancy, even allowing for measurable risk factors. But the Harvard study does not adjust for income, arguing that the people in the study – health professionals and nurses -are broadly doing the same job. But, judging from the heated discussion that seems to accompany this topic, the argument will go on.