What is your 'effective age'?
As of the 23rd May 2022 this website is archived and will receive no further updates.
understandinguncertainty.org was produced by the Winton programme for the public understanding of risk based in the Statistical Laboratory in the University of Cambridge. The aim was to help improve the way that uncertainty and risk are discussed in society, and show how probability and statistics can be both useful and entertaining.
Many of the animations were produced using Flash and will no longer work.
How old are you?
You might, quite reasonably, calculate your chronological age as the time elapsed since you were born. But what is the effective age of your body?
If you want to find out, you can go to many websites which will tell you your ‘real age’, such as this one by Doctor Oz, or your 'health age', ‘vitality age’, or ‘biological age’.
For all these calculators, you put in various characteristics of your health and habits, and out pops an assessment of say your biological age or health age. But what does this age mean? And where do they get it from? In the rush to try and persuade you to act more healthily, or to sell you products or services, this is generally not explained.
One way to define your effective age is as the age of a ‘healthy’ person who has the same risk profile as you do. So if your chronological age is 50, but your effective age is 60, this means that your poor lifestyle and so on has put you in the same risk category as a 60-year old who has ‘healthy’ risk factors, at least the ones that are potentially modifiable.
Figure 1 shows the basic idea: a trajectory of a typical healthy person is constructed, and then your risk level is mapped across to the find the age of such a healthy person with the same level.
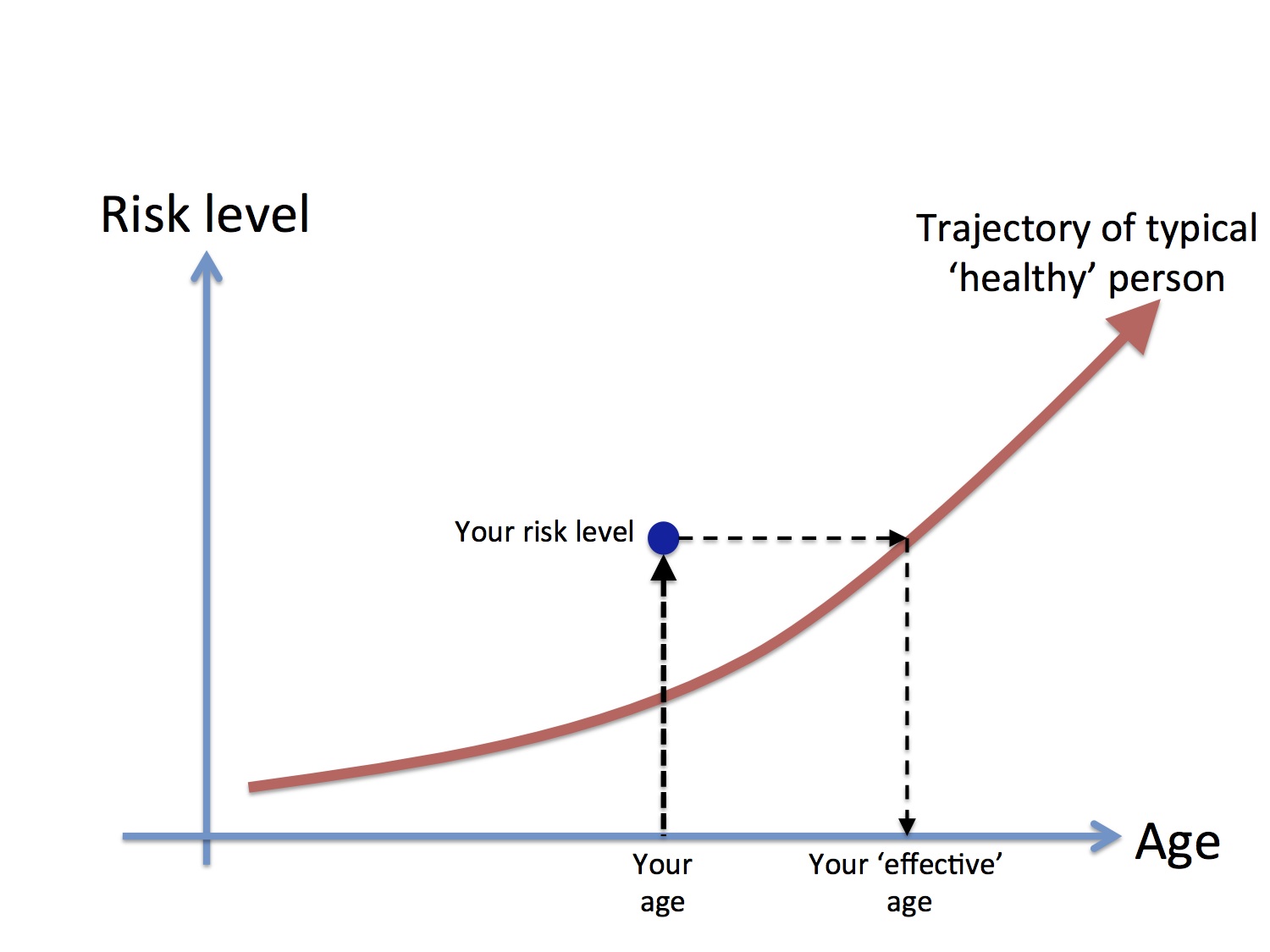
Figure 1. Generic interpretation of your 'effective age'
Sometimes the formal basis for these calculations is provided. For example, your Ubble Age is the age of an average person of the same gender who matches your risk of dying in the next 5 years.
How old are your organs?
The same idea can be used for individual bits of your body. In particular, many cardio-vascular risk calculators will tell you your ‘heart age’ or a 'vascular age'. These have recently been reviewed, and some examples include -
- The new NHS Heart Age, based on the JBS3 calculator: this is the age of a person of same gender and ethnicity, who has healthy risk factors, and the same annual risk of heart attack or stroke as you (NB I had a hand in producing this).
- Both the UK Heart Age calculator and QRISK give the age of a person with healthy risk factors the same 10-year cardiovascular risk as you (assuming you don't die of some other cause during this period).
- The New Zealand 'Know your Numbers' program finds someone with the same 5-year cardiovascular risk as you (again assuming you don't die of some other cause during this period).
Although different calculators find the age of someone who matches your annual, 5-year or 10-year cardio-vascular risk, we'll see below that, under reasonable conditions, this choice does not make a difference to your heart age.
The idea of lung-age goes back 30 years to a classic paper of 1985: using updated equations, calculators derive the age for which your lung function results would be expected in a typical person of your age and height. And Public Health England are apparently developing a brain age calculator.
How does your behaviour affect your effective age?
It would be simplest to be told how many years certain behaviours add or subtract from your effective age, for example smoking 20 a day adds 9 years to your effective age, however old you are at the moment. It turns out that this attractive idea can be made reasonably rigorous.
First we need to go back to the basis for working out mortality risk: the 'hazard' curve. Figure 2 shows the annual risk of death for an average person during each year of age in England and Wales – this is known as the annual hazard or, more traditionally, the ‘force of mortality’.
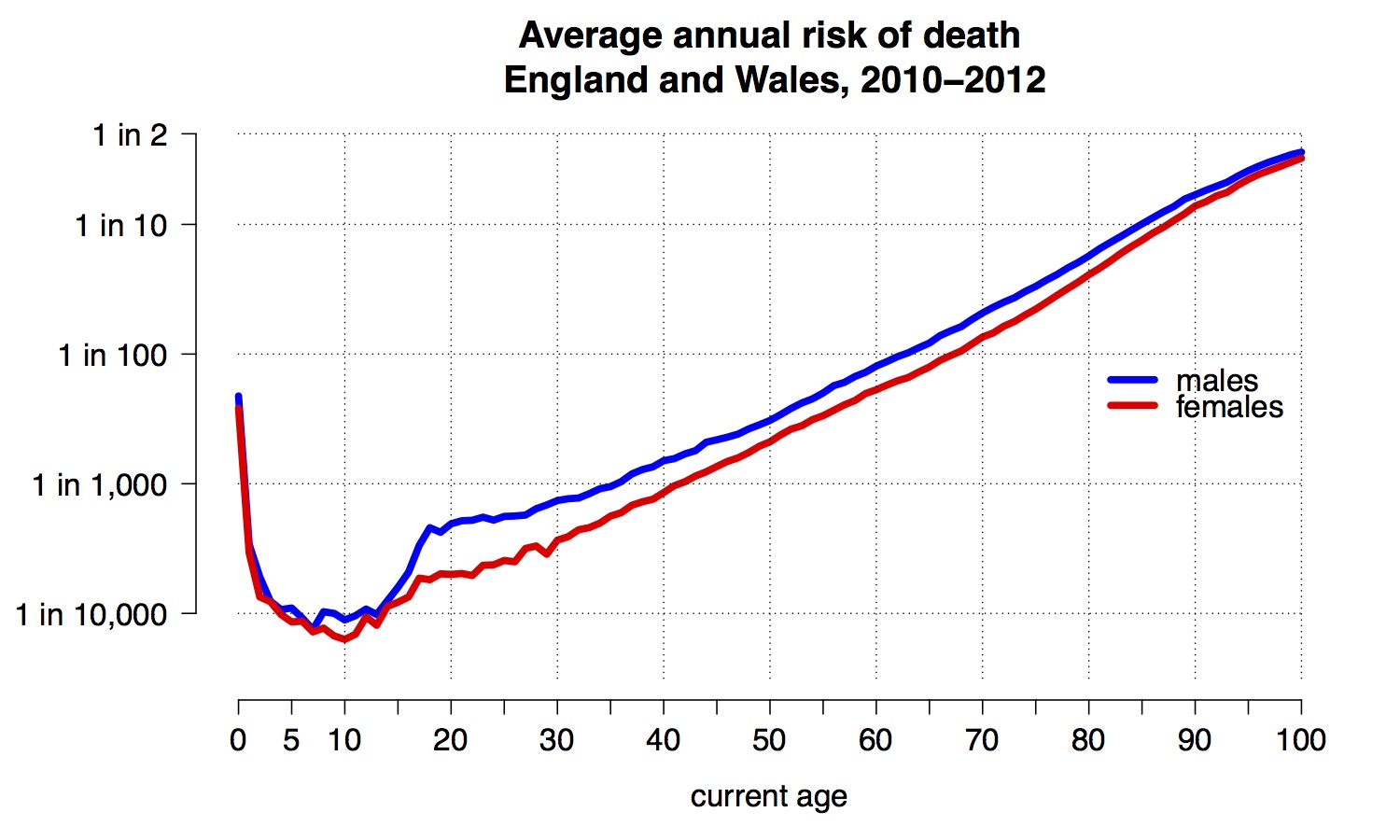
Figure 2: the annual risk of death for an average person during each year of age in England and Wales: note the vertical axis is on a logarithmic scale
We note the steep decline once one has survived early childhood, to a minimum of less than 1 in 10,000 at around 10 years old – in spite of the anxieties expressed about our vulnerable children, nobody in the history of humanity has been as safe as a modern 10-year-old. Then, apart from a ‘risk-taking’ bulge between 15 and 25, there is a reasonably straight line until around 95. This linear growth on a logarithmic scale corresponds to an exponential growth in annual hazard, meaning the risk of dying each year increases by a fixed proportion for each year we age. We can check this by plotting the ratio of hazards for adjacent years, as shown in Figure 3.
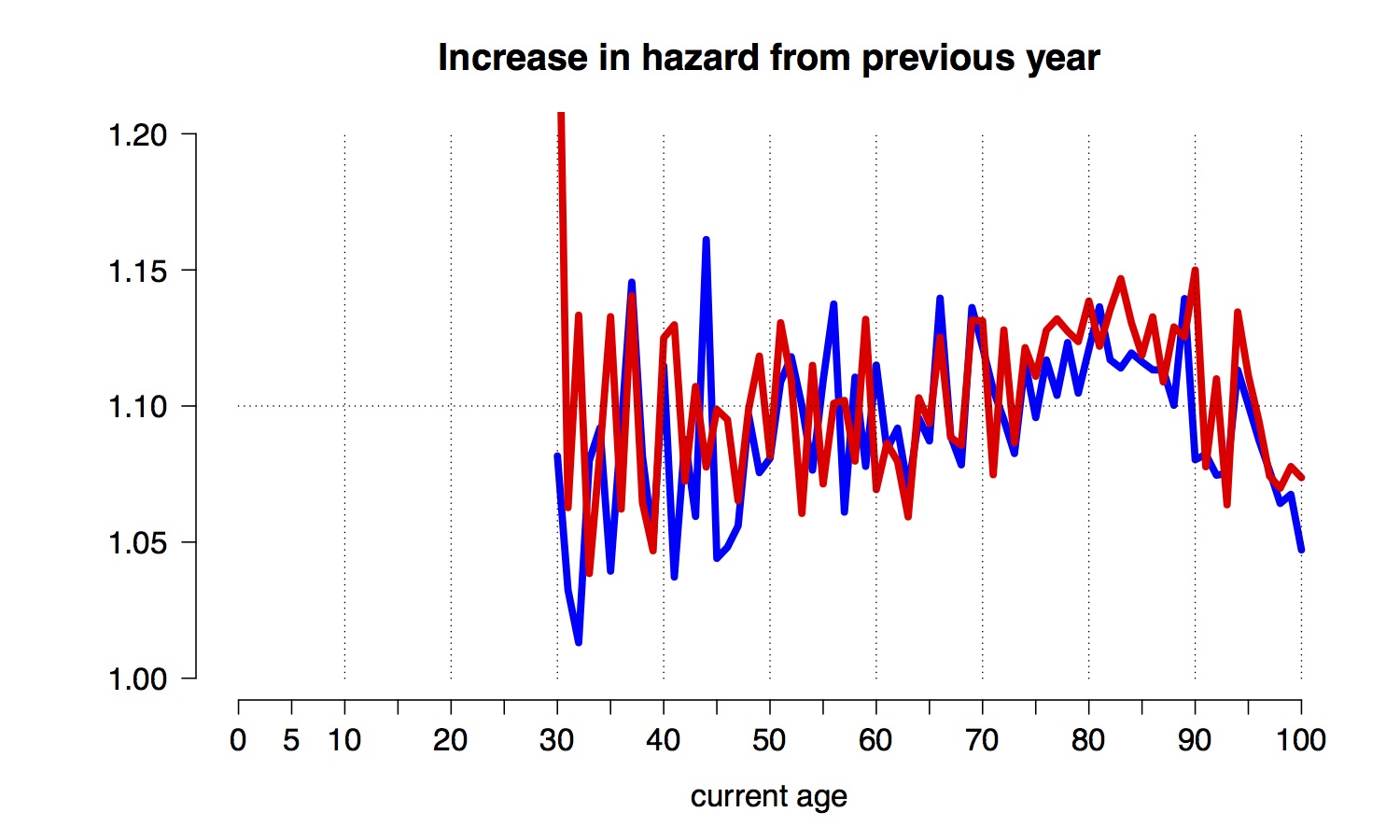
Figure 3: ratio of annual hazards in adjacent years of age
The relative increase is fairly constant between 30 and 95 - this was recognised by Benjamin Gompertz back in 1825. Roughly, the increase in annual hazard associated with ageing one year is around 1.1 – essentially your chance of dying before your next birthday increases by around 10% for each year you age, whether you are a man or a woman. Equivalently, your risk doubles roughly every seven years.
Demographers have concluded that this ratio seems to be remarkably constant across individuals and over time. This can provide a simple basis for ‘effective age’ calculations.
A standard output from epidemiological studies is the ‘estimated all-cause mortality hazard ratio’, which is the increased annual risk of death for those with the risk factor compared to those without. The estimated are derived from Cox regression and apply over the range of ages being studied.
Table 1 provided some examples from some recent epidemiological studies.
| Behaviour | Hazard ratio | Change in effective age (years) | Comments and reference |
|---|---|---|---|
| Smoking 20 a day | 2.20 | + 8 | Doll and Peto |
| Eating 50g processed meat a day | 1.18 | + 2 | Around 3 rashers of bacon per day - EPIC. |
| Watching 2 hours TV a day | 1.08 | + 1 | EPIC |
| BMI: an extra 5 Kg/m^2 above 25 Kg/m^2 | 1.29 | + 3 | Around 1 year for each 5 extra Kg PSC |
| Minimal exercise | 0.82 | - 2 | Compared to inactivity: EPIC |
| Further exercise | 0.92 | - 1 | Compared to minimal: EPIC |
| Fruit and vegetables | 0.90 | - 1 | High vs low: EPIC |
| Statins | 0.91 | - 1 | High-risk but without CVD |
The crucial insight is that these hazard ratios can be translated into ‘change in effective years’. Suppose $h$ is the hazard ratio associated with a risk factor. Assume that each increased year of age is associated with a hazard ratio $r$, where $r \approx 1.1$ from Figure 2. Then the increased risk associated with the risk factor is equivalent to being a change in $t$ years of your effective age if
$$ r^t = h$$
or equivalently
$$ t = \frac{\log h}{\log r}.$$
Since $\log r \approx 0.1$, we have that
$$ t = 10 \log h.$$
Applying this formula to the risk factors in Table 1 provides the values in the column headed ‘Change in effective age’.
Translating each risk factor into a change in effective age provides a simple, but fairly rigorous form of communication: for example, two hours TV a night is associated with the same risk as if you were 1 year older. I wish I could say that this neat result was original, but after I started using it I found that the idea had already been fully developed in a wonderful 1993 paper by Brenner and colleagues on ‘rate advancement periods’.
So there is a reasonably sound basis for the sort of ‘real-age’ calculations shown on websites, although I suspect the numbers used may often be more guesswork than based on the latest epidemiology. And even if the numbers for individual behaviours in the table are reasonable, it neither means we can simply add them up, and or that we can necessarily gain those lost years by changing our behaviour.
So what's the impact of using these ideas?
Concepts such as effective age are clearly attractive and even gripping metaphors: a journalist recently listed the 'age' of each of their organs, and it is claimed that 27,000,000 people have been provided with their RealAge.
There is also some evidence that these ideas might help change behaviour and improve risk factors. The recent review claims that “vascular age is easily understood by patients and has a greater impact on care than presenting an estimated CVD risk score”, citing a study in which Heart Age "was more emotionally impactful in those participants at higher actual CVD risk levels". And a trial randomised over 3,000 subjects to either conventional medical advice, a risk score or Heart Age, and found that “after 12 months of follow-up, levels of metabolic parameters had improved significantly in both risk communication groups, but most profoundly in the heart age group. Furthermore, heart age had increased in the control group and decreased in the intervention groups”
Using essentially the same analysis, change in effective age can also be interpreted as advancing the time that you may suffer an adverse event. A study used such Rate Advancement Periods (RAPs) to communicate increased heart-attack risk from hypertension (RAP = 8 years) and smoking (RAP =11 years), saying the "RAP may be interpreted as that, on average, smokers are expected to advance their risk of myocardial infarction approximately 11 years compared with never/former smokers". The authors "encourage the use and evaluation of the RAP as an effective risk communication tool in actual counselling situations".
The Step2quit study found double the quit-rates in smokers who were told their lung age (6% vs 14%), and this led to recommendations to routinely use this concept. However a recent study has cast doubt on the ability of lung-age to increase motivation, while it's been suggested that the concept may even reduce motivation to quit for those with a ‘normal’ lung age.
This all points to the need for randomised trials of alternative methods of providing risk information, for example comparison with other metaphors such as hazard ratios, changes in life-expectancy, and ‘microlives’.
Appendix: When can we ignore your current age and the risk horizon?
The difference between your chronological and your effective age has been called the 'years lost' - for example if you are 50 years old, but your effective age is 60, you have 'lost' 10 years. We've seen in the examples above that for common behaviours we can assume that the 'years lost' does not depend on how old you are.
We've also seen that 'heart-age' might depend on whether we consider your risk of a heart attack this year, over the next 5 years, or the next 10 years, and it would be much nicer if this risk 'horizon' were irrelevant.
It turns out that there are reasonable conditions under which each both these simplifying conditions hold: your years lost do not depend on your current age, and your effective age does not depend on the risk horizon. Both these hold provided -
- The 'proportional hazards' model: i.e. factors act on the baseline trajectory by increasing the annual risk by a percentage that does not depend on current age. This is the standard assumption in the Cox regression model used widely in epidemiological studies
- The risk of a healthy person increased exponentially with age, i.e. each year the risk increases by a fixed percentage.
Fortunately, as we've seen in the section above, both these conditions will, at least approximately, hold in many situations.
Let $T$ be the age at which an adverse event $E$ happens to an individual, and let $S(t;x)$ be the survivor function at age $t$ for someone with risk factors $x$, i.e. $S(t;x) = P(T >t; x) $, the probability that the adverse event in question has not occurred by age $t$.
Suppose the 'risk level' $r$ of a person aged $t_1$ with risk factors $x_1$ is defined as the probability of the event first occurring to them within the next $k$ years. so that
$$r = P( t_1 \lt T \lt t_1+k \,|\, T \gt t_1 ;x_1) = \frac{P(t_1 \lt T \lt t_1+k ; x_1) }{P( T \gt t_1 ; x_1)} = \frac{S(t_1;x_1) - S(t_1+k;x_1)}{S(t_1;x_1) }.$$
Suppose a 'healthy' person has risk factors $x_0$. Then the effective age $t_0$ of the individual in question is the age at which a healthy person has risk $r$ of experiencing the event in the next $k$ years, and so, as before,
$$r = P( t_0 \lt T \lt t_0+k \,|\, T \gt t_0 ; x_0) = \frac{P(t_0 \lt T \lt t_0+k ; x_0) }{P( T \gt t_0 ; x_0)} = \frac{S(t_0;x_0) - S(t_0+k;x_0)}{S(t_0;x_0) },$$
and so
$$ \frac{S(t_1;x_1) - S(t_1+k;x_1)}{S(t_1;x_1) } = \frac{S(t_0;x_0) - S(t_0+k;x_0)}{S(t_0;x_0) },$$
or equivalently
\begin{equation}
\frac{S(t_1+k;x_1)}{S(t_1;x_1) } = \frac{S(t_0+k;x_0)}{S(t_0;x_0) }.
\end{equation}
Let $h(t;x)$ be the hazard function at age $t$ for an individual with risk factors $x$, where $h$ is the instantaneous risk of $E$ occurring given it has not occurred up to age $t$. Thus $h(t;x) = p(t;x)/S(t;x)$, the cumulative hazard $H(t;x) = \int h = - \log S(t;x)$, and so $S(t;x) = e^{-H(t;x)}.$
Therefore, in terms of the cumulative hazard, we obtain the identity
\begin{equation}
H(t_1+k;x_1) - H(t_1;x_1) = H(t_0+k;x_0) - H(t_0;x_0).
\end{equation}
which provides a general, although implicit, definition of the effective age $t_0$.
We now introduce the first assumption - that of proportional hazards. This means the hazard function can be expressed as $h(t;x) = h_0(t) e^{-\beta x}$, where $h_0$ is a baseline hazard function, essentially that for $x=0$. Thus $H(t;x) = H_0(t) e^{-\beta x}$ for a cumulative baseline hazard $H_0$.
We thus get the identity
\begin{equation}
\left( H_0(t_1+k) - H_0(t_1) \right) e^{\beta x_1} = \left( H_0(t_0+k) - H_0(t_0) \right) e^{\beta x_0} .
\end{equation}
or equivalently
\begin{equation}
\log \left( H_0(t_0+k) - H_0(t_0) \right) = \log \left( H_0(t_1+k) - H_0(t_1) \right) + \beta (x_1 - x_0) .
\end{equation}
We now bring in the second assumption - that the hazard is exponentially increasing. We can express this as $h_0(t) = a e^{-bt}$, the Gompertz equation. With the proportional hazard assumption, this means that $h(t;x) = a e^{\beta x} e^{-bt}$, so the risk factors just have the effect of increasing the constant.
GIven this assumption, we see that
$$H_0(t_1+k) - H_0(t_1) = \int_{t_1}^{t_1+k} h_0(t) dt = a \int_{t_1}^{t_1+k} e^{-bt} dt = \frac{a}{b} e^{bt_1} \left[ e^{bk} -1 \right].$$
Substituting this into the general implicit equation for $t_1$ gives the simple form
\begin{equation}
b t_1 = b t_0+ \beta (x_1 - x_0),
\end{equation}
or equivalently
\begin{equation}
t_1 = t_0+ \frac{\beta}{b} (x_1 - x_0),
\end{equation}
we immediately see that
- the lost years $t_1 - t_0$ does not depend on the current age,
- the effective age $t_1$ does not depend on $k$, and so the risk horizon is irrelevant.
We note that for binary exposures $x_1 - x_0 =1$, and hence the 'years lost' is $\frac{\beta}{b}$: this is also the Rate Advancement Period. It can be estimated by fitting both the exposure and age as covariates in a Poisson regression, and then taking the ratio of their coefficients. Alternatively, in a Cox regression, exposure and age-at-entry can be fitted as covariates, and time-in-study used as the time variable, as in this recent paper.
- Log in to post comments
