Squaring the square, in glass

As of the 23rd May 2022 this website is archived and will receive no further updates.

understandinguncertainty.org was produced by the Winton programme for the public understanding of risk based in the Statistical Laboratory in the University of Cambridge. The aim was to help improve the way that uncertainty and risk are discussed in society, and show how probability and statistics can be both useful and entertaining.

Many of the animations were produced using Flash and will no longer work.

Submitted by david on Tue, 22/01/2013 - 6:24pm

Here is my latest stained glass effort, seen on a snowy day.

trinity-glass2-small.jpg

It is a 'square of squares', where all the constituent squares are of different sizes. Here are the dimensions -

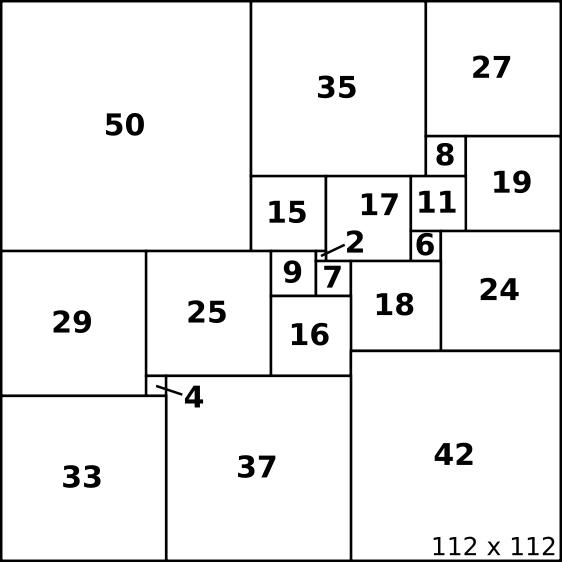
sqsqbig.png

It is copied from the logo of the Trinity Mathematical Society, who point out that it is the unique smallest simple squared square (smallest in that it uses the fewest squares, and simple in that no proper subset of the squares of size at least 2 forms a rectangle). It was proved to be the smallest such square by Duijvestijn in 1978, but this was by exhaustive computer search, which seems a bit like cheating.

There is a fine Wikipedia site which contains more than you ever wish to know about squaring-the-square.

Challenge

I wanted to only use 4 colours without any square touching another of the same colour, and of course I knew this is possible due to the 4-colour theorem. But I wanted the four large outer squares to be 'white' (in order to increase the Mondrian appeal). It took some effort and trial-and-error to find a 4-colouring with this property. Are there others?

Comments

Perhaps

Fri, 01/02/2013 - 4:31pm

All 6 permutations of red/green/blue are solutions anyway. Here I have another (six) solution(s): http://www.bilder-hochladen.net/files/kf5d-1-c4ca-jpg.html I guess there are even more solutions (maybe 6 or 12). My starting point were field 9,17, which must be the same colour and 29,37, which also must be the same colour (which can be different from 9,17 of course).

Perhaps

Fri, 01/02/2013 - 4:36pm

P.S: 6 more solutions are given by exchanging red/white of fields 6,11 in my previous solution.

whuber

Wed, 06/02/2013 - 4:29pm

There are 28 * 6 solutions found with an exhaustive search in Mathematica (0.3 seconds computing time). 28 of them are visible in an array at http://imgur.com/iT4jdf2: yours is in the second row, rightmost column. The other 28 * 5 solutions can be obtained by permuting {red, green, blue}.

david

Wed, 06/02/2013 - 5:19pm

A beautiful array. It is tempting to try a vast stained glass window featuring all of these!

Perhaps

Wed, 06/02/2013 - 6:50pm

Field 11 and 19 are the same colour in 14 plots (3rd, 4th row), which is not allowed.

whuber

Wed, 06/02/2013 - 9:20pm

Thank you for catching that. Although I visually checked the answers, for some reason I didn't see that erroneous part. No problem, though: my code represents the squares as an abstract graph; I merely omitted the edge between squares 11 and 19. In other words, the algorithm is fine, but the input was deficient. Upon inserting the missing edge, the computation time is reduced to 0.08 seconds and the number of solutions is reduced to 14 * 6 (it certainly cannot be increased!). You can see the basic 14 solutions arrayed at http://imgur.com/3YXGWaM. I believe David's is the very last one in the array. They all look ok to me, but if anyone should see any more errors, I would be happy to fix them up. BTW, I posted the code at http://mathematica.stackexchange.com/questions/19177/strategies-for-solving-problems-involving-searches (along with a simpler example to illustrate its workings).

jhodsdon

Thu, 26/09/2013 - 4:31pm

In approximately 25 minutes, I found 6 other possibilities using trial and error. I created an album online at http://imgur.com/a/CpYQp with them all.