Numbers and the common-sense bypass

Yesterday the Sunday Times [paywall] covered a talk Anne Johnson and I had given at the Cheltenham Science Festival about the statistics of sex, and the article said

more people are having sex in their teens, roughly 30% before the age of 16.

Let’s leave aside whether this is an accurate statistic or not, and simply look at what happened when the Daily Mail lifted this material into an article of its own. They made a number of errors, but the cracker was when the statement by the Sunday Times got turned into the remarkable headline:

30 per cent of total sexual encounters take place before 16.

And just in case they change their website, here is the evidence (4th bullet point):

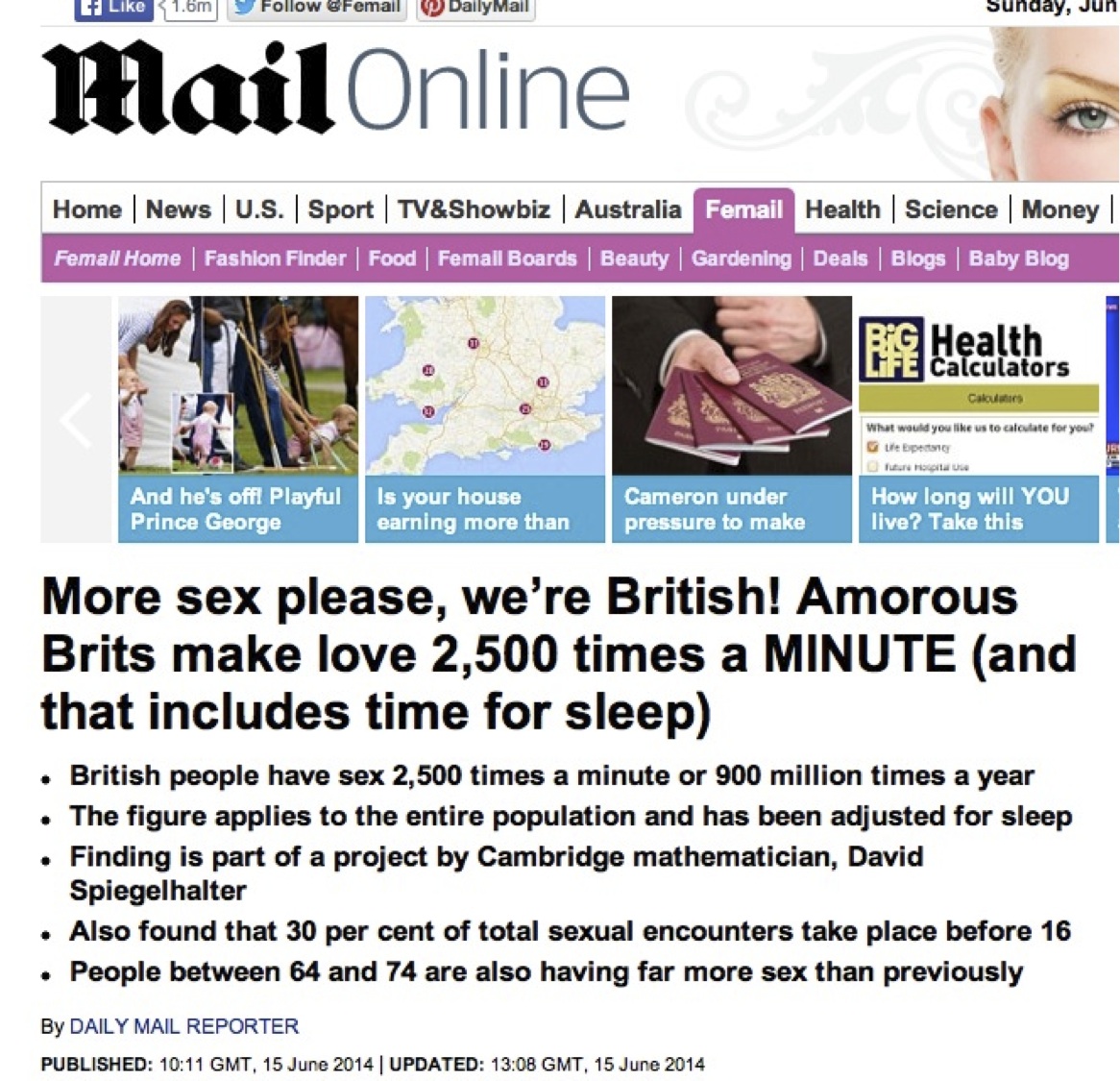
A little reflection should show that the Mail’s statement is more than implausible. 30% of all sex occurring before 16? Just think about it. The Daily Mail clearly didn't.

For those that would like some evidence, the article reports my estimate, based on the National Survey of Sexual Attitudes and Lifestyles (NATSAL), that male+female couples in Britain have sex around 900,000,000 times a year. So if if 30% of this were in the under 16’s, that would be about 300,000,000 times a year. There are about 1,500,000 14 and 15 year olds, that’s 750,000 potential couples, so to get to this total they would all have to be having sex 400 times a year, which is more than once a day. No wonder they don’t have time for homework. Or maybe this number is just ridiculous.

This could be just an enthusiastic sub-editor, such as the one who produced the wonderful headline below

- this was rapidly changed to the more reasonable “Bikers involved in more than one third of serious Kent road accidents“, but not before someone had grabbed the previous version.

But in the Mail’s case it was not just the sub-editor who wrote the headline – the journalist made the claim in the article. So how can such an idiotic statement appear in a national newspaper?

This is not intended to be a standard ‘aren’t the media hopelessly innumerate’ bash, fun though those are. I am genuinely interested in how intelligent people can write such statements without seeming to engage their common sense (which I generously assume they have).

Perhaps the first thing to note is that the two errors above are both of an identical logical nature – the so-called ‘transposed conditional’. Let's consider some pairs of statements, the first of which is reasonable, the second is in error:

• 30% of people, when they were aged under 16, had sex
• 30% of sex happens with people aged under 16

• One third of fatal accidents involved motorcyclists
• One third of motorcyclists have fatal accidents

• 90% of women with breast cancer get a positive mammography
• 90% of women with a positive mammography have breast cancer

(In fact, the current breast screening leaflets point out that fortunately only around 25% of women with a positive mammography have breast cancer).

In more abstract terms, what happens is that the “proportion of A that are also B”, is reported as “the proportion of B that are also A”. This is also known as the Prosecutor’s Fallacy , as it is a mistake made in legal cases. It is extremely dangerous to mix up the statements

• The probability of the evidence, if the suspect is innocent, is 1 in 1,000,000
• The probability of the suspect being innocent, given this evidence, is 1 in 1,000,000

and yet this mistake has happened repeatedly, if implicitly.

[See additional comment at the bottom of this article, added June 18th]

One argument is that it is simple innumeracy: the so-called ‘deficit model’ explanation, that could be counteracted by better education in the mechanics of mathematics. But I am sure that most of us who make these kind of mistakes (and I am not excluding anyone here, including me) are functionally numerate, and could even have a stab at working out a 15% tip.

Another argument is that this really not an issue with numeracy, but a simple error in logic. And yet it might be reasonable to assume that a journalist, or a judge, would not confuse the following two statements

• All dogs are furry mammals with 4 legs
• All furry mammals with 4 legs are dogs.

So maybe it is something in the middle: an inability to combine reason with numbers, some kind of paralysis that comes when confronted with numerical arguments that means that ordinary common sense is bypassed. I see this when tutoring young people for GCSE maths: intelligent kids who when asked to do some maths couched as a pseudo-real-world problem, (“Fred travels at 50 mph for 30 minutes, how far does he go?”) go into a mental panic, start using formulae at random, and come up, like Baldrick doing mental arithmetic, with some absurd answer (“1500 miles”). And yet if I asked them the same problem in the real-real-world, and did not say it was maths, they would be able to get the answer by using some basic reasoning (“25 miles”). The kind of maths teaching promoted by Tim Gowers on how maths should be taught to non-mathematicians seeks to avoid this ‘find the formula and plug in the numbers’ style, and with luck the Core Maths curriculum will feature more reasoning with practical situations.

One consequence of this inability to take a sensible critical attitude to numbers is that opinions are pushed to the extremes: numbers are to be either accepted, and even fetishised, as some sort of God-given truth, or rejected out of hand as ‘just statistics’. Possibly in the same breath. Just listen to the Today programme or Question Time.

Of course there are other areas in which common sense is bypassed - when we may be only too willing to suspend our normal powers of criticism and warmly embrace delusion. These include claims for alternative therapies, arguments by populist politicians, optimistic prognoses for desperately ill loved-ones, or bigging up England’s performance in the World Cup. Sadly, in all these cases some realism may be more appropriate.

Additional comment added June 18th

An equivalent way to view this error is in terms of the 'wrong denominator': is the 30% a proportion of people, or of all sexual activity? Gerd Gigerenzer emphasises that these mistakes are due to not being clear about the 'reference class', i.e. 30% of what?. Ambiguity can be avoided by always making the class clear by saying, for example, "Out of every 100 people reaching 16, 30 have already had sex".