The Maths of Paul the “Psychic” Octopus
As of the 23rd May 2022 this website is archived and will receive no further updates.
understandinguncertainty.org was produced by the Winton programme for the public understanding of risk based in the Statistical Laboratory in the University of Cambridge. The aim was to help improve the way that uncertainty and risk are discussed in society, and show how probability and statistics can be both useful and entertaining.
Many of the animations were produced using Flash and will no longer work.
England’s performance in the World-Cup last summer was thankfully overshadowed by the attention given to Paul the Octopus, who was reported as making an unbroken series of correct predictions of match winners. Here we present a mathematical analysis of Paul’s performance in an attempt to answer the question that (briefly) gripped the world: was Paul psychic?
First let’s look at the evidence. Paul, resident of Oberhausen Sea World in Germany but originally from Weymouth, likes eating mussels. His keepers lowered a pair of open-topped boxes into his tank before each match, each containing a mussel and labelled with the flag of the country of one the competing teams. Paul then squoozed his way into one of the boxes and ate a mussel: the country whose box was entered was declared as Paul’s prediction. He had previously made predictions in Germany’s six matches in the Euro 2008 competition, but picked Germany’s box each time giving rise to suggestions that he was attracted to the German striped flag. Four out of 6 of these predictions were correct. But he excelled himself in the World Cup – he picked the winner of all Germany’s 7 matches, including their two defeats, and then got the World Cup final correct too. Paul’s Wikipedia page contains more details than you need to know.
Let’s start by taking the evidence at face value, and denote it $\hbox{8 right}$ for the 8 matches he apparently correctly predicted. We consider this as a question of deciding between two competing hypotheses: $H_{\rm psy}$, that Paul is a psychic marvel; $H_{\rm oct}$ that he is just an ordinary rubbery octopus. Evidence influences the relative plausibility of two competing hypotheses through the likelihood ratio, which is the ratio of the probability of the evidence given Paul is psychic, that is $p( \hbox{8 right} |H_{\rm psy})$, to the probability of the evidence given he is not, $p( \hbox{8 right} |H_{\rm oct}) $, where the vertical line ‘|’ corresponds to `given’. Now if we assume that being psychic means he has perfect predictive powers, then $p( \hbox{8 right} |H_{\rm psy}) =1$, since he is certain to predict all the matches correctly. But if we assume that his choice is pure luck, then he has made 8 independent correct predictions, each with probability ½, and so $p( \hbox{8 right} |H_{\rm oct}) = \frac{1}{2^8} = 1/256$. So the ‘naïve’ likelihood ratio in favour of being psychic is
apparently rather powerful evidence. In fact the evidence is even stronger than this, since in the first three matches there was a possibility of a draw, so that the chance of a correct prediction is around 3/8. But we shall ignore this nicety.
But is this likelihood ratio appropriate? It depends on two assumptions. The first is that we do not allow Paul to be just a little bit psychic – he’s either right every time or guessing. The second assumption is that the chance of making a correct prediction is ½ for each match. This will only be the case if this is a fair and unbiased trial, so that a non-magical mollusc has an equal chance of selecting either team. But numerous web discussions have suggested this might not be the case: possible biases include a preference for certain flags, preference for the right-hand box, where he is in the tank when the boxes are lowered in, and so on. It was even suggested that he was filmed many times and just one film chosen. But of course, as the predictions were released before each match, then being able to fiddle Paul’s choice only helps if someone else feels they can predict the results: clearly this would be almost as remarkable as if Paul could make perfect predictions. It might be a reasonable strategy to somehow persuade Paul to the pick the favourite team for each match, this did not always happen.
Paul’s main rival was Mani the Parrokeet in Singapore, who was roundly beaten by Paul in the psychic showdown after picking Netherlands to win the final. In fact many animals around the world were making predictions – porcupines, guinea pigs and so on. Maybe we are only hearing about the successful one, and any creature picking North Korea to win the Cup is doomed to obscurity. This is a very important factor in interpreting evidence – what are we not hearing? When we see someone hit a hole-in-one on Youtube we know that this piece of film was chosen from countless unsuccessful attempts. But like Sherlock Holmes and the dog that did not bark in the night, such missing evidence is often difficult to identify but can be vital. This is a well-known problem in interpreting claims about medical treatments – if we only hear about the successes, the evidence only tells us that it could possibly work, not how likely it is to work. That’s why registers of clinical trials are being established so unsuccessful studies cannot just disappear.
Paul rose to international prominence after 4 predictions, and we can assume that we would have never heard about him if he had got any wrong. So suppose there are $n$ animals making such predictions. Out of $n$ sets of predictions made by utterly un-psychic creatures, the chance that at least one gets them all right is
$P(\hbox{at least one of the predictors gets 4 matches right})$
$= 1 – P(\hbox{none of the predictors gets 4 matches right})$
$=1 – P(\hbox{all of the predictors get at least one wrong})$
$= 1 – P(\hbox{a predictor gets at least one wrong})^n$
$ = 1 – (1 – P(\hbox{a predictor gets 4 right})^n)$
$ = 1 – \left(1- \frac{1}{16}\right)^n$
$ = 1 – \left(\frac{15}{16}\right)^n$
If there were say 20 animals making predictions at random, the chance that at least one gets all 4 predictions right is therefore
$1 – (15/16)^{20} = 1 – 0.28 = 0.72$. So there is at least a 2 in 3 chance of someone like Paul popping up by chance alone. This means that the first four matches provide almost no evidence supporting Paul's powers, and only the final four predictions count, giving a likelihood ratio of 16.
Let's ignore this for the moment and take the ‘$ \hbox{8 right} $’ evidence at face value. So far we have looked at the probability of the evidence given Paul being psychic or not psychic, but this does not get to the heart of the matter. There is an even more important issue that arises when we try to calculate the quantity that we are really interested in - the probability of Paul being psychic given the evidence, that’s $p( H_{\rm psy} | \hbox{8 right} )$.
It turns out that it is convenient to work in terms of odds rather than probabilities, where odds = probability / (1 – probability), so that a probability of say 0.8 corresponds to odds of 4, and odds of 1/3 corresponds to a probability of 0.25. We therefore want the odds of being psychic given the evidence, which is $p(H_{\rm psy}| \hbox{8 right} )/ p(H_{\rm oct}| \hbox{8 right} )$, where $p(H_{\rm oct}| \hbox{8 right} ) = 1- p(H_{\rm psy}| \hbox{8 right} )$ is the probability of not being psychic given the evidence. To get this we use the odds form of Bayes theorem:
This says that that the initial (also known as the ‘prior’ ) odds of being psychic, $ p(H_{\rm psy})/p(H_{\rm oct})$, before we see the evidence, is changed into the final (also known as the ‘posterior’) odds, after seeing the evidence, by multiplying by the likelihood ratio. This way of changing our beliefs in the light of experience was published by the Reverend Thomas Bayes in 1763, 2 years after his death. It is a basic consequence of the rules of probability, and provides the basis for theories of learning, spam filters, formal legal reasoning, and an entire school of statistical inference.
The bottom line is that we first need to provide the initial probability on Paul being psychic. What, before you heard about his exploits, would have been your belief that an octopus could predict football results? Quite low, I believe. Let’s give Paul the benefit of the doubt and say that the initial probability is $p( H_{\rm psy}) = 1/100.$ The initial odds is therefore 1 / 99, and the final odds, taking the evidence from all 8 matches at face value, is 256 / 99 = 2.6 , which translates to a final probability $p( H_{\rm psy}| \hbox{8 right}) = 256/355 = 0.72$, not much more than 50:50. Similar Bayesian processing of evidence can be used in legal reasoning, but has also been used to assess the probability that the Turin Shroud truly shows the face of Christ, that a recently discovered tomb was that of Christ, and even that God exists (answer: 67%), although the accuracy of these analyses is open to some dispute, to put it mildly.
But would we be happy with this analysis of Paul’s supernatural skills? In fact, zero might be a more reasonable figure for the prior probability, if we simply consider it impossible that an octopus can predict football results. But if $p( H_{\rm psy} )$=0, then the initial odds is 0, and the final odds is 0 whatever the size of the likelihood ratio. This is an important mathematical result: if you believe that a hypothesis is impossible, then no amount of evidence will change your mind, and you have to put the events down to just chance. I think that’s how everyone felt.
Going deeper
Let $q$ be the probability that Paul can correctly forecast the result of a football game. We have assumed so far that Paul is either always correct ($q=1$) or it is all just chance ($q=\frac{1}{2}$). But any value of $q$ that is different from $\frac{1}{2}$ is interesting, since this would at least imply that Paul is ‘psychically-inclined’ even if he wasn’t infallible. We shall see what the evidence tells us about what $q$ might be.
We shall just take the final 4 correct predictions, on the basis that we would not even have heard of Paul if he had not got the first 4 right. For each $q$, the chance of getting 4 out of 4 right is $q^4$. Suppose we were generous enough to think, before hearing about Paul’s successes, that all values of $q$ were equally likely. Then with a bit of Bayesian statistics we can show that our belief about $q$ should follow a probability distribution $p(q|data) = 5 q^4$, which is drawn in Figure 1.
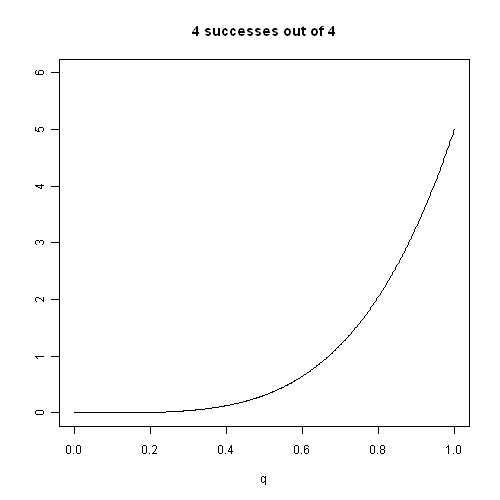
Figure 1. Probability distribution for $q$, Paul's chance of successfully selecting a winning team, after observing 4 successes out of 4 attempts.
The most likely value for $q$ is 1, but the distribution has mean 5/6, which we would assess to be the probability that he would get the next match right - this is an example of Laplace’s Law of Succession.
Laplace also showed that, before observing Paul’s performance, we should think that the each possible number of successful predictions is equally likely, that is $\frac{1}{5}$ chance on getting each of 0,1,2,3,4 right. The likelihood ratio for comparing the two hypotheses, just-chance vs psychically-inclined, is therefore $\frac{1}{5}/ \frac{1}{16}$ = 3.2. So if we previously had around 1% probability that Paul could be psychically-inclined, then our posterior probability would be around 3%.
Our final belief about $q$ would therefore have a great lump on ½ with size 97%, with the remaining 3% following the distribution shown in Figure 1. Personally, I still have a 100% lump on ½.
- Log in to post comments

Comments
Anonymous (not verified)
Tue, 15/02/2011 - 8:47pm
Permalink
probability theory
Anonymous (not verified)
Wed, 13/04/2011 - 11:09pm
Permalink
Thanks!
PeterJThomas
Mon, 27/06/2011 - 8:21am
Permalink
Mainstream media
SP (not verified)
Thu, 21/07/2011 - 1:44pm
Permalink
A small query
dude (not verified)
Mon, 12/09/2011 - 2:26pm
Permalink
keep on petting these animals