Is the Lottery biased?

In Lottery Expectations we looked at the observed and theoretical distributions for the total count of times each number has come up, and the gap between a number's appearances. Here we explain the mathematics behind the theoretical distribution of counts, and how to check for true randomness, and derive the theoretical distribution for gaps.

The distribution for the number of times each number has been drawn

We first need to introduce some notation. Let the number of balls chosen at each draw be $m=6$, and the number of balls in the 'bag' be $M=49$. Each number between 1 and 49 therefore has a $p=m/M=6/49$ chance of being chosen at a particular draw. Therefore after $D$ draws, the total number of times each ball has been drawn has a Binomial distribution with parameters $p$ and $D$.

This distribution has mean $Dp$ and variance $Dp(1-p)$, and can be approximated by a Normal distribution with matching mean and variance. This is what is done in the animation.

Testing for bias in the lottery

There are many test statistics that are designed to identify different ways in which the lottery draws may not be entirely random, such as favouring odd or even numbers and so on Haigh1997. We consider the simplest possible: an adapted chi-square test.

After $D$ draws, we expect any particular number $j$ to have occurred $E_j = Dp = Dm/M$ times, which in the UK lottery corresponds to $6D/49 \approx D/8$ So, for example, after 1000 draws we would expect each number to have been chosen around 125 times. If after $D$ draws we add up the total number of times each number has occurred, and label these totals $O_1,...,O_{49}$, then a naive chi-squared statistic compares the observed and expected counts using the standard formula
$$ X^2_{\rm naive} =\sum_{j=1}^{j=M} \frac{(O_j - E_j)^2}{E_j},$$
which would be compared to a theoretical $\chi^2$ distribution with $M-1=48$ degrees of freedom. For those not familiar with chi-squared tests, this statistic will be large if the observed counts are very different from the expected, since then the numerators $(O_j - E_j)^2$ will be very big. However we would never expect the observed to exactly match the expected, due to chance variation, and it turns out that if the numbers really are drawn at random then the statistic should be approximately 48, if we assume all the balls being drawn were statistically independent.

However, as Haigh (1997) points out, this would only be the case if all $mD$ individual ball-draws were independent, which is not the case as 6 balls are drawn without replacement at each lottery-draw. Hence it is impossible, for example, for a particular number to be drawn as ball 2 and 6 within a single draw. This lack of independence requires an adjustment to the chi-squared statistic above, so that the correct statistic is
$$ X^2 = \frac{(M-1)}{(M-m)}X^2_{\rm naive};$$
hence the adjustment factor multiplies the naive chi-squared statistic by a factor 48/43 $\approx$ 1.12. This adjusted statistic is shown in the lottery animation.

If we group the lottery draws in sets of 50, we can plot the $X^2$ statistics for successive groups. This is shown below, with the lower and upper 2.5\% points of a $\chi^2_{48}$ distribution drawn in, respectively 30.8 and 69.0.

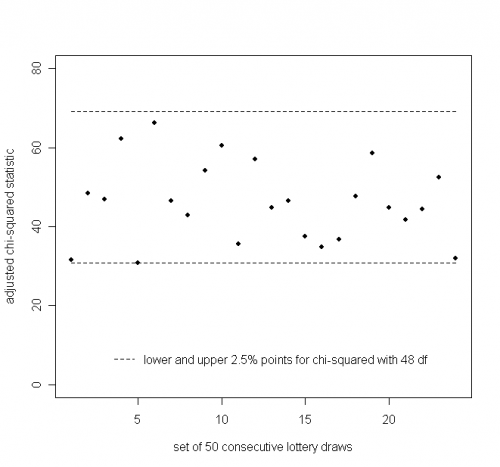
We see that all the 24 statistics lie inside the central 95\% interval for the $\chi^2_{48}$ distribution.

The distribution of gaps between a number's appearances

Suppose a specific number $j$ has just been drawn. Then suppose that we label successive draws a ‘success’ if $j$ is drawn, a ‘failure’ otherwise: the chance of a ‘success’ is defined as $p$ which in this case is 6/49. Let $X$ be the number of failures before the first success, i.e. the ‘gap’ before $j$ is drawn again. The chance of a $X=0$ is the same as the chance of $j$ appearing in the next draw, which is $p = 6/49 \approx 0.12$. The chance of a gap of 1 is the same as the chance of a single 'failure' and then a 'success', which is $(1-p)p = 43/49 \times 6/49 = 0.11 $, and so on. Therefore the chance of $X$ taking on any particular value $x$ is the same as the chance of observing a series of $x$ ‘failures’ followed by a single ‘success’, so that
$$ {\rm Pr}(X=x) = (1-p)^x p.$$
This is the Geometric distribution: note that sometimes this distribution is defined as the time until the first success, which here corresponds to $Y=X+1$. The mean of this distribution is $1/p - 1 = 49/6 – 1 = 7.16$, so the average gap length is around 7.

The maximum gap in the whole lottery history

We observed a maximum gap of 72 for ball number 17 between February and November 2000, which seems extraordinarily long. Is this surprising?

The chance of any particular gap being at least $x$, ie ${\rm Pr}(X \ge x)$, is simply the chance of observing $x$ failures in a row, so that
$${\rm Pr}(X \ge x) = (1-p)^x.$$
Therefore the chance of observing a gap as long as 72 is $(43/49)^{72}$ = 0.000082 , or around 1 in 12,500, which seems very rare indeed. If after number 17 was drawn in February 2000, we had specifically said 'let's wait until 17 appears again', then we would have been justifiably amazed at having to wait 73 draws until it did appear again, and might even suspect it had been left out of the bag! However we did not pre-specify this particular gap as being interesting, and simply chose it as the largest of 7440 observed gaps. Therefore a crude estimate of such a rare event occurring, when there are 7440 opportunities for it to occur, is $0.00082 \times 7440 = 0.61$. A more accurate estimate is obtained by noting that, if there are $n$ independent gaps,

$$\begin{array}{rl}{\rm Pr( maximum-gap }\ge x)&= 1- {\rm Pr( maximum-gap } since the probability that all gaps are less than $x$ is the product of $n$ identical probabilities that a single gap is less than $x$. Hence we would estimate the probability of a maximum gap being at least 72 as $1 - (1 - 0.000082)^{7440} = 0.46$. This result suggests that 72 is not in the least surprising.

However, as with the $\chi^2$ statistic above, this distribution theory is not quite correct as there is some dependence between the gaps induced by there being exactly 6 numbers selected at each draw. We can therefore conduct a simulation with the results shown before and reproduced below.

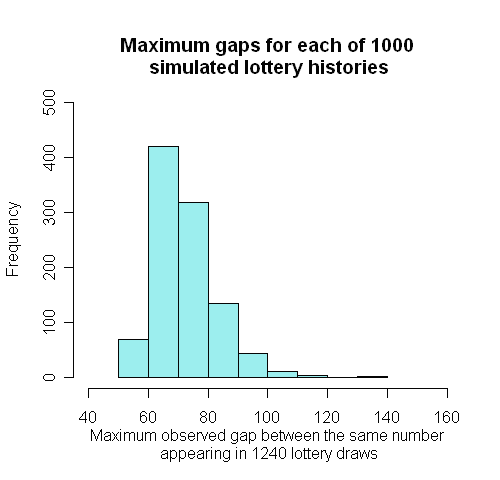
In 1000 simulations of 1240 draws, the mean largest gap was 72 , 154 was largest gap, 42% were 72 or more (showing the approximation assuming independence, 0.46, is quite accurate). Therefore our maximum gap of 72 is almost exactly what one would expect.

Further reading and links

This discussion is primarily based on Haigh (1997) whose notation we use.