Another tragic cluster - but how surprised should we be?

Sadly another passenger plane crashed yesterday - the third in 8 days, the Air Algerie flight on July 24th, the TransAsia flight in Taiwan on July 23rd, and Malaysian Airlines in Ukraine on July 17th. Does this mean that flying is becoming more dangerous and we should keep off planes? The following analysis may appear cold-hearted, but is not intended to diminish the impact of this tragic loss on the people and families involved.

The Plane Crash Info website contains the summaries of these three accidents - this site makes powerful reading and is not for those with a fear of flying. Their Statistics page is full of useful information, including a graph showing a clear decline in the rate of accidents over the last 40 years: the 9/11 events in 2001 do not even make a blip in the graph.

However, it shows that flying can still carry some danger. 91 commercial flights containing 18 or more passengers have crashed in the previous 10 years (2004 to 2013), a rate of one every 40 days on average. So how surprising is it that 3 should happen in a space of 8 days?

A similar question was asked last November, when 6 cyclists were killed in London over 2 weeks, and Jody Aberdein and I wrote a paper on this: the methods are explained here. We can apply the same ideas to the 'cluster' of plane crashes, although of course this analysis is rather simplistic and ignores the undoubted variation in risk when flying in different parts of the world.

Consider any window of 8 days. If planes crash in an entirely unpredictable way at a rate of 91 over 10 years (3650 days), then we would expect 8 * 91/3650 = 0.2 crashes in any particular 8-day window. So assuming a Poisson distribution, the chance of at least 3 crashes in an 8-day window is around 1 in 1000 - very small indeed. So it is very surprising that there would be 3 or more crashes between July 17th and July 25th 2014.

But this is not the right question to ask. We should be concerned with whether such a 'cluster' is surprising over some period, say 10 years. In 10 years there are 456 non-over-lapping 'windows' of 8 days, and the chance that at least one of these contains at least 3 crashes = 1 - the chance that that none of them has at least three crashes = 1 - 0.999^456 = 0.41 (without rounding). And the more complex 'scan-statistic' adjustment, that allows for a sliding rather than non-overlapping windows, puts this chance up to 0.59.

So there is around a 6 in 10 chance that we should see such a large cluster over a 10-year period. In fact, as the graph below shows, the most likely maximum number of crashes of commercial planes with over 18 passengers in any 8-day window over 10 years is exactly ..... 3.

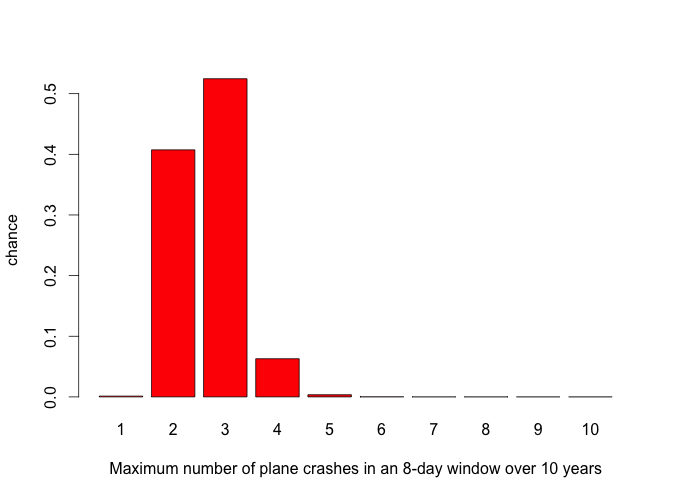
It is difficult to know how to interpret this - our emotions are rightly influenced by the awful nature of these events and the suffering they have caused. But personally, I hope it will make me no more nervous about flying than I am at the moment (and I have to admit I am not that keen to start with).

[Edit 10.02 July 25th: I had initially stated the adjusted probability stayed at 0.41: on checking the code I realised it changed to 0.59]